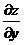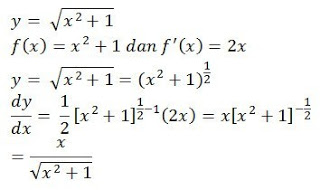Fungsi Implisit

Fungsi Implisit

Turunan fungsi Implisit – Apa yang dimaksud fungsi implisit ? yaitu fungsi yang memuat dua variabel  atau lebih,  variabel-variabel tersebut terdiri dari variabel bebas dan variabel tidak bebas, biasanya variabel-variabel tersebut dinyatakan dalam x dan y dimana variabel x dan y terletak didalam satu ruas sehingga tidak dapat dipisahkan menjadi ruas yang berbeda (baca : ruas kiri dan ruas kanan) seperti halnya fungsi eksplisit.

Turunan Fungsi Implisit  Serta bentuk umum nya
Secara umum bentuk  turunan fungsi implisit  adalah f(x,y) = 0, mencari turunan fungsi implisit sama dengan mencari solusi bentuk umumnya dan prinsipnya tidak jauh berbeda dengan mencari turunan fungsi biasa.
Untuk lebih jelasnya Perhatikan contoh-contoh soal dibawah ini, bagaimana mencariturunan fungsi implisit.

Contoh Soal dan Pembahasan Turunan Fungsi Implisit
Tentukan   dari setiap fungsi Implisit dibawah ini!

[Penyelesaian]
Turunkanlah kedua ruas terhadap x,

[Penyelesaian]
Turunkanlah kedua ruas terhadap x,

[penyelesaian]
Turunkanlah kedua ruas terhadap x

 

[Penyelesaian]

Turunkanlah kedua ruas terhadap x

[Penyelesaian]
Turunkanlah kedua ruas terhadap x

 [Penyelesaian]
Turunkanlah kedua ruas terhadap x

 [Penyelesaian]
Turunkanlah kedua ruas terhadap x

Turunan Fungsi Dua Variabel

TURUNAN FUNGSI DUA (2) VARIABEL

TURUNAN PARSIAL 

Diketahui   z = f(x,y) fungsi  dengan dua variabel independen x dan y.  Karena  x dan y independen maka :

   1.  x  berubah-ubah sedangkan y tertentu.
   2 . y  berubah-ubah sedangkan x tertentu.

DEFINISI
a. Turunan parsial terhadap variabel x
     Jika  x  berubah-ubah  dan y  tertentu        maka  z  merupakan fungsi x, Turunan        parsial  z = f(x,y) terhadap x  sbb :

  

b. Turunan parsial terhadap variabel y

    Jika  y berubah-ubah  dan x  tertentu        maka z  merupakan fungsi y,  Turunan          parsial  z = f(x,y) terhadap y  sbb :

Fungsi dua peubah atau lebih dapat ditulis dalam bentuk eksplisit atau implisit. 
Jika fungsi dua peubah dinyatakan dalam bentuk eksplisit, maka secara umum ditulis dalam bentuk z = F(x,y).
Sebaliknya jika fungsi dituliskan dalam bentuk implisit, secara umum  ditulis dalam bentuk F(x,y,z) = 0.
nggak
Contoh:
z = 2x + y
xy + xz – yz = 0

c. Turunan Parsial Fungsi Dua dan Tiga Peubah
            Misal z = F(x,y) adalah fungsi dengan variable bebas x dan y.
Karena x dan y variable bebas maka terdapat beberapa kemungkinan yaitu:

• y dianggap tetap, sedangkan x berubah-ubah.
• x dianggap tetap, sedangkan y berubah-ubah
• x dan y berubah bersama-sama sekaligus.

            Pada kasus 1 dan 2 diatas mengakibatkan fungsinya menjadi fungsi satu peubah, sehingga fungsi tersebut dapat diturunkan dengan menggunakan definisi turunan pertama yang telah dipelajari pada kalkulus diferensial.

           Misal z = F(x,y) adalah fungsi dua peubah yang terdefinisi pada interval tertentu, turunan parsial pertama z terhadap x dan y dinotasikan dengan

     & 
   
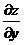
       Untuk memudahkan persoalan andaikan z = F(x,y) maka untuk menentukan  sama artinya dengan menurunkan variabel x dan variabel y dianggap konstan dan selanjutnya y diturunkan. Demikian pula untuk menentukan  sama artinya dengan menurukan variable y dan variable x dianggap konstant lalu diturunkan.

            Dengan cara yang sama, andaikan W = F(x,y,z) adalah fungsi tiga peubah yang terdefinisi dalam selang tertentu maka turunan parsial pertama dinyatakan dengan , dan yang secara berturut didefinisikan oleh :

d. Differensial Total dan Turunan Total
     Membentuk turunan parsial  dan, perubahan dan  ditinjau berasingan.sekarang kita tinjau pengaruh perubahan x dan y bersama-sama. Dalam Persamaan linier dari  dan berbentuk  disebut diferensial total dari z dititik
9( x,y).
jika z = f (x,y)mempunyai turunan parsial pertama yang kontinu di D ,maka z mempunyai diferensial total :

dz =  disetiap titik (x,y) dari D

Turunan Fungsi Satu Variabel

TURUNAN FUNGSI SATU VARIABEL

TURUNAN FUNGSI ( 1 VARIABEL )

              Turunan fungsi (diferensial) ialah fungsi lain dari suatu fungsi sebelumnya, misalnya fungsi f menjadi f’ yang memiliki nilai tak beraturan. Turunan ( diferensial ) dipakai sebagai suatu alat untuk menyelesaikan berbagai masalah dalam geometri dan mekanika.
              Konsep turunan sebagai bagian utama dari kalkulus dipikirkan pada saat yang bersamaan oleh Sir Isaac Newton ( 1642 – 1727 ), ahli matematika dan fisika bangsa Inggris dan Gottfried Wilhelm Leibniz ( 1646 – 1716 ), ahli matematika bangsa Jerman.

Misal y ialah fungsi dari x atau y = f(x). Turunan (atau diferensial) dari y terhadap x

persamaan y = 4x maka nilai dari turunan tersebut menurut definisi di atas adalah

RUMUS RUMUS TURUNAN FUNGSI 
MATEMATIKA

Rumus 1 : Jika y = cxn dengan c dan n konstanta real , maka dy/dx = cn xn-1

contoh :
y = 2x4maka dy/dx = 4.2x4-1 = 8x3
kadang ada soal yang pakai pangkat pecahan atau akar

y = 2√x = 2x1/2 turunannya adalah 1/2.2 x (1/2-1)= x -1/2= 1/√x

Rumus 2 : Jika y = c dengan c adalah konstanta maka dy/dx = 0

contoh :
jika y = 6 maka turunannya adalah sama dengan nol (0)

Rumus 3 : Jika y = f(x) + g(x) maka turunannya sama dengan turunan dari masing-masing fungsi = f'(x) + g'(x)

contoh :
y = x3+ 2x2maka y’ = 3x2+ 4x
y = 2x5+ 6 maka y’ = 10x4+ 0 = 10x4

Rumus 4 : Turunan Perkalian Fungsi Jika y f(x).g(x) maka y’ = f'(x) . g(x) + g'(x) . f(x)

contoh :
y = x2(x2+2) maka
f(x) = x2
f'(x) = 2x
g(x) = x2+2
g'(x) = 2x
kita masukkan ke rumus y’ = f'(x) . g(x) + g'(x) . f(x)
y’ = 2x (x2+2) + 2x . x2
y’ = 4x3+ 4x

Rumus 5 : Turunan Pembagian Fungsi

contoh :

Rumus 6 : jika kamu punya y = [f(x)]nmaka turunannya adalah n [f(x)]n-1. f'(x)

contoh :

Rumus 7 : Turunan Logaritma Natural misal y = ln f(x) maka turunannya

contoh :

Rumus 8 : ef(x) maka,  dy/dx = ef(x).f'(x)

contoh :
y = e2x+1
f(x) = 2x+1
f'(x) = 2
maka f’ = e2x+1 . 2
             = 2e2x+1

Rumus 9 : Turunan Trigonometri Sin
Jika kamu punya y = sin f(x) maka turunannya adalah y’ = cos f(x) . f'(x)

contoh :
y = sin(x2 + 1) maka
y’ = cos (x2+1) . 2x
     = 2x. cos (x2+1)

Rumus 10 : Turunan Trigonometri Cos
Jika kamu punya y = cos f(x) maka turunanya adalah y’ = -sin f(x). f'(x)

contoh :
y = cos (2x+1) maka turunannya
y’ = -sin (2x+1) . 2
     = -2 sin (2x+1)

RUMUS TURUNAN KE DUA 

rumus turunan kedua sama dengan turunan dari turunan pertama (sobat turunkan sebanyak dua kali). Turunan kedua sobat peroleh dengan menurunkan turunan pertama.

Contoh :
Turunan kedua dari x3+ 4x2
turunan pertama = 3x2+ 8x
turunan kedua = 6x + 8

Limit Fungsi

Pengertian

Di dalam matematika, konsep limit digunakan untuk menjelaskan sifat dari suatu fungsi, saat argumen mendekati ke suatu titik, atau tak hingga; atau sifat dari suatu barisan saat indeks mendekati tak hingga. Limit digunakan dalam kalkulus (dan cabang lainnya dari analisis matematika) untuk mencari turunan dan kekontinyuan.

Limit fungsi adalah salah satu konsep mendasar dalam kalkulus dan analisis, tentang kelakuan suatu fungsi mendekati titik masukan tertentu. Suatu fungsi memetakan keluaran f(x) untuk setiap masukan x. Fungsi tersebut memiliki limit L pada titik masukan p bila f(x) “dekat” pada L ketika x dekat pada p.

Teorema Limit

Definisi dan Teorema Limit. Limit dalam bahasa umum bermakna batas. Ketika belajar matematika beberapa guru yang menyatakan bahwa limit merupakan pendekatan. Definisi dari limit ini menyatakan bahwa suatu fungsi f(x) akan mendekati nilai tertentu jika x mendekati nilai tertentu. Pendekatan ini terbatas antara dua bilangan positif yang sangat kecil yang disebut sebagai epsilon dan delta. Hubungan ke-2 bilangan positif kecil ini terangkum dalam definisi limit.

Cara Mengerjakan Limit Fungsi yang Tidak Terdefinisi

Ada saatnya penggantian nilai x oleh a dalam lim f(x) x→a membuat f(x) punya nilai yang tidak terdefinisi, atau f(a) menghasilkan bentuk 0/0, ∞/∞ atau 0.∞. Jika terjadi hal tersebut solusinya ialah bentuk f(x) coba sobat sederhanakan agar nilai limitnya dapat ditenntukan.

Limit Bentuk 0/0

Bentuk 0/0 kemungkinan timbul dalam

ketika kita menemukan  bentuk seperti itu coba untuk utak-utik fungsi tersebut hingga ada yang bisa dicoret. Jika itu bentuk persamaan kuadrat kita bisa coba memfaktorkan atau dengan cara asosiasi dan jangan lupakan ada aturan a2-b2 = (a+b) (a-b). Berikut adalah contohnya :

Bentuk ∞/∞

Bentuk limit  ∞/∞ terjadi pada fungsi suku banyak (polinom) seperti

Contoh Soal
Coba kalian tentukan

Jawaban

Berikut merupakan rangkuman rumus cepat limit matematika bentuk  ∞/∞

jika m<n maka L = 0
jika m=n maka L = a/p
jika m>n maka L = ∞

Bentuk Limit (∞-∞)

Bentuk (∞-∞) sering sekali muncul pada saat ujian nasional. Bentuk soalnya sangat beragam. Namun, penyelesaiannya tidak jauh-jauh dari penyederhanaan. Berikut contoh soal yang akan kami ambil dari ujian nasional 2013.

Tentukan Limit

Jika kalain masukkan x -> 1 maka bentuknya akan mmenjadi (∞-∞). Dan untuk menghilangkan bentuk ∞-∞ kita sederhanakan bentuk tersebut menjadi,

Rumus Cepat menyelesaikan limit tak terhingga

Rumus cepat mengerjakan limit tak terhingga yang pertama dapat digunakan untuk bentuk soal limit tak terhingga pada bentuk pecahan. Untuk memperoleh nilai limit tak terhingga bentuk pecahan kita hanya perlu memperhatikan pangkat tertinggi dari masing-masing pembilang dan penyebut.
ada 3 kemungkinan yang dapat saja terjadi. Pertama, pangkat tertinggi pembilang lebih kecil dari pangkat tertinggi penyebut. Kedua, pangkat tertinggi pembilang sama dengan pangkat tertinggi penyebut. Ketiga, pangkat tertinggi pembilang lebih tinggi dari pangkat tertinggi penyebut. Rumus ke-3 nilai limit tak terhingga bentuk pecahan tersebut dapat dilihat pada persamaan dibawah ini.