TURUNAN FUNGSI ( 1 VARIABEL )
Turunan fungsi (diferensial) ialah fungsi lain dari suatu fungsi sebelumnya, misalnya fungsi f menjadi f’ yang memiliki nilai tak beraturan. Turunan ( diferensial ) dipakai sebagai suatu alat untuk menyelesaikan berbagai masalah dalam geometri dan mekanika.
Konsep turunan sebagai bagian utama dari kalkulus dipikirkan pada saat yang bersamaan oleh Sir Isaac Newton ( 1642 – 1727 ), ahli matematika dan fisika bangsa Inggris dan Gottfried Wilhelm Leibniz ( 1646 – 1716 ), ahli matematika bangsa Jerman.
Misal y ialah fungsi dari x atau y = f(x). Turunan (atau diferensial) dari y terhadap x
persamaan y = 4x maka nilai dari turunan tersebut menurut definisi di atas adalah
RUMUS RUMUS TURUNAN FUNGSI
MATEMATIKA
Rumus 1 : Jika y = cxn dengan c dan n konstanta real , maka dy/dx = cn xn-1
contoh :
y = 2x4maka dy/dx = 4.2x4-1 = 8x3
kadang ada soal yang pakai pangkat pecahan atau akar
y = 2√x = 2x1/2 turunannya adalah 1/2.2 x (1/2-1)= x -1/2= 1/√x
Rumus 2 : Jika y = c dengan c adalah konstanta maka dy/dx = 0
contoh :
jika y = 6 maka turunannya adalah sama dengan nol (0)
Rumus 3 : Jika y = f(x) + g(x) maka turunannya sama dengan turunan dari masing-masing fungsi = f'(x) + g'(x)
contoh :
y = x3+ 2x2maka y’ = 3x2+ 4x
y = 2x5+ 6 maka y’ = 10x4+ 0 = 10x4
Rumus 4 : Turunan Perkalian Fungsi Jika y f(x).g(x) maka y’ = f'(x) . g(x) + g'(x) . f(x)
contoh :
y = x2(x2+2) maka
f(x) = x2
f'(x) = 2x
g(x) = x2+2
g'(x) = 2x
kita masukkan ke rumus y’ = f'(x) . g(x) + g'(x) . f(x)
y’ = 2x (x2+2) + 2x . x2
y’ = 4x3+ 4x
Rumus 5 : Turunan Pembagian Fungsi
contoh :
Rumus 6 : jika kamu punya y = [f(x)]nmaka turunannya adalah n [f(x)]n-1. f'(x)
contoh :
Rumus 7 : Turunan Logaritma Natural misal y = ln f(x) maka turunannya
contoh :
contoh :
y = e2x+1
f(x) = 2x+1
f'(x) = 2
maka f’ = e2x+1 . 2
= 2e2x+1
Rumus 9 : Turunan Trigonometri Sin
Jika kamu punya y = sin f(x) maka turunannya adalah y’ = cos f(x) . f'(x)
contoh :
y = sin(x2 + 1) maka
y’ = cos (x2+1) . 2x
= 2x. cos (x2+1)
Rumus 10 : Turunan Trigonometri Cos
Jika kamu punya y = cos f(x) maka turunanya adalah y’ = -sin f(x). f'(x)
contoh :
y = cos (2x+1) maka turunannya
y’ = -sin (2x+1) . 2
= -2 sin (2x+1)
RUMUS TURUNAN KE DUA
rumus turunan kedua sama dengan turunan dari turunan pertama (sobat turunkan sebanyak dua kali). Turunan kedua sobat peroleh dengan menurunkan turunan pertama.
Contoh :
Turunan kedua dari x3+ 4x2
turunan pertama = 3x2+ 8x
turunan kedua = 6x + 8





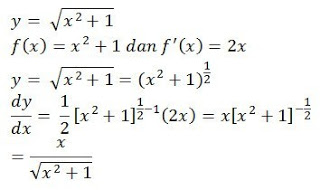



Tidak ada komentar:
Posting Komentar