MATRIKS (Lanjutan)
Determinan
Pengertian determinan :
Determinan merupakan sebuah bilangan tunggal atau scalar, dan hanya dijumpai dalam matriks bujur sangkar. Jika determinan suatu matriks bujur sangkar adalah nol, maka matriks tersebut dikatakan sebagai matriks singular. Dan jika determinan matriks tersebut bukan nol, maka matriks tersebut dikatakan sebagai matriks non singular. Matriks nonsingular, secara linear tidak tergantung (saling independent)
Determinan Matriks Ordo 2 x 2
Jika diberikan matriks ordo 2 dinyatakan seperti bentuk di bawah.
Sifat-sifat Determinan :
Sifat-sifat determinan ada enam, yaitu :
a. Determinan suatu matriks sama dengan determinan dari transposenya, det (A) = det (A^t).
Contoh :
b. Penambahan atau pengurangan suatu kelipatan bukan nol dari suatu baris/kolom dari baris/kolom lainnya tidak akan mempunyai pengaruh pada determinan.
c. Penukaran tempat antara dua baris atau kolom sembarang dari suatu matriks akan merubah tanda, tetapi tidak merubah harga absolut dari determinan.
Contoh :
d. Determinan dari suatu matriks segitiga (triangular matriks), yaitu matriks dengan elemen-elemen nol diatas atau di bawah diagonal utama, adalah sama dengan hasil kali dari elemenelemen dari diagonal utama.
Contoh :
e. Jika semua elemen dari suatu baris atau kolom adalah nol, determinan adalah nol.
Contoh :
f. Jika dua baris atau kolom identik, atau proporsional, yaitu secara linear tergantung, maka determinan adalah nol.
Contoh :
METODE MINOR DAN KOFAKTOR
Salah satu cara menentukan determinan matriks segi adalah denga minor-kofaktor elemen matriks tersebut.
Cara ini dijelaskan sebagai berikut:
Misalkan adalah suatu matriks yang diperoleh dengan cara menghilangkan baris ke-i dan kolom ke-j dari suatu matriks .
Didefinisikan sebagai berikut:
- Minor elemen diberi notasi , adalah .
- Kofaktor elemen , diberi notasi , adalah .
Contoh:
Misalkan suatu matriks A berukuran 3x3 seperti berikut ini:
maka diperoleh:
Definisi: Misalkan suatu matriks A = dan kofaktor elemen , maka:
Ekspansi Laplace
Metode atau ekspansi Laplace adalah suatu cara untuk menghitung determinan dengan menggunakan kofaktor.
Determinan dari suatu matriks = jumlah perkalian elemen-elemen dari sembarang baris/kolom dengan kofaktor-kofaktornya.
Ekspansi Laplace dapat ditulis dengan cara :
|A| = a11|C11|+a12|C12|+a13|C13| menggunakan baris 1
Dengan pola yang sama dapat juga dihitung dengan menggunakan baris ke dua dan ketiga, dengan memberikan hasil determinan yang sama.






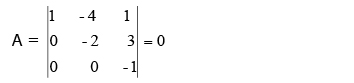




Tidak ada komentar:
Posting Komentar