MATRIKS I

MATRIKS 

Dalam matematika, matriks adalah susunan bilangan, simbol, atau ekspresi, yang disusun dalam baris dan kolom sehingga membentuk suatu bangun persegi.Pemanfaatan matriks misalnya dalam menemukan solusi sistem persamaan linear. Penerapan lainnya adalah dalam transformasi linear, yaitu bentuk umum dari fungsi linear, misalnya rotasi dalam 3 dimensi. Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Dimensi matriks dapat berupa 2 x 3 (dua baris dan tiga kolom), 3 x 2 (tiga baris dan dua kolom) , 3 x 3 (tiga baris dan tiga kolom) dan lain-lain. Pada umumnya, matriks ditulis dalam tanda kurung siku atau kurung kurawal ”.

Operasi Dasar Matriks

Penjumlahan dan Pengurangan Matriks

Penjumlahan dan pengurangan matriks hanya bisa dilakukan jika kedua matriks memiliki ukuran atau tipe yang sama. Elemen-elemen yang dijumlahkan atau dikurangi adalah elemen yang posisi atau letaknya sama.

Penjumlahan Matriks

Pengurangan Matriks

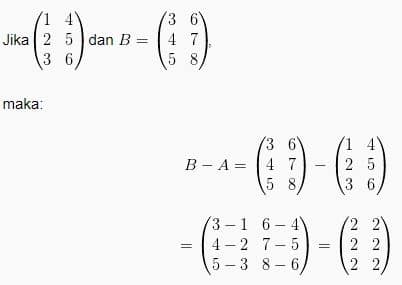
Sifat penjumlahan dan pengurangan matriks, diantaranya yaitu:
A + B = B + A
(A + B) + C = A + (B + C)
A – B ≠ B – A

Perkalian Matriks

Matriks dapat dikalikan dengan bilangan bulat maupun dengan matriks lain. Setiap perkalian matriks, memiliki syarat masing-masing, diantaranya yaitu:

a. Perkalian Matriks Dengan Bilangan Bulat atau Perkalian Skalar Matriks

Matriks bisa dikalikan dengan bilangan bulat, maka hasil perkalian tersebut berupa matriks dengan elemen-elemennya yang merupakan hasil kali antara bilangan dan elemen-elemen matriks tersebut. Jika matriks A dikali dengan bilangan r, maka r.A =(r.aij). Contohnya:

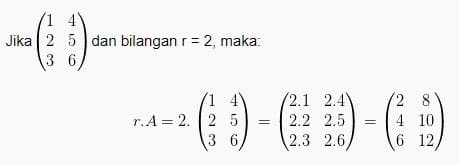
Perkalian matriks dengan bilangan bulat dikombinasikan dengan penjumlahan atau pengurangan matriks bisa dilakukan pada matriks dengan ordo sama. Berikut sifat-sifat perkaliannya:

r(A + B) = rA + rB
r(A – B) = rA – rB

b. Perkalian Dua Matriks

Perkalian antara dua matriks misalnya matriks A dan B, bisa dilakukan jika jumlah kolom A sama dengan jumlah baris B. Perkalian tersebut menghasilkan matriks dengan jumlah baris sama dengan matriks A dan jumlah saman dengan matriks B, sehingga:

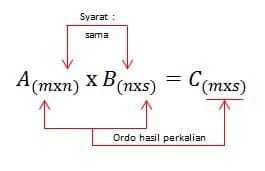
Elemen-elemen matriks C(mxs) merupakan penjumlahan dari hasil kali elemen-elemen baris ke-i matriks A dengan kolom ke-j matiks B. Berikut skemanya:

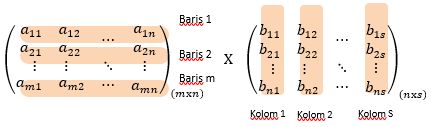
Misalnya matriks A berordo (3 x 4) dan matriks B berordo (4 x 2), maka matriks C berordo (3 x 2). Elemen C pada baris ke-2 dan kolom ke-2 atau a22 diperoleh dari jumlah hasil perkalian elemen-elemen baris ke-2 matriks A dan kolom ke-2 matriks B. Contohnya:

Perlu diingat sifat perkalian dua matriks bahwa:

A x B ≠ B x A

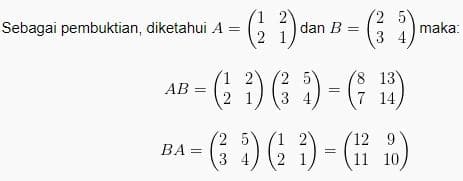
Terbukti bahwa A x B ≠ B x A. Ada sifat-sifat lain perkalian matriks dengan bilangan atau dengan matriks lain, sebagai berikut:

k(AB) = (kA)B
ABC = (AB)C = A(BC)
A(B + C) = AB + AC
(A + B)C = AC + BC

MACAM - MACAM MATRIKS 

Matriks memiliki berbagai macam bentuk, diantaranya yaitu:

1. Matriks Baris

Matriks Baris yaitu merupakan matriks yang hanya terdiri dari satu baris saja.

Contoh :

P = [3 2 1]

Q = [4 5 – 2 5]

2. Matriks Kolom

Matriks Kolom yaitu merupakan matriks yang hanya terdiri atas satu kolom saja.

Contoh :

Matriks Kolom

3. Matriks Persegi

Matriks Persegi yaitu merupakan matriks yang banyak baris sama dengan banyak kolom. Jika banyak baris matriks persegi A adalah n maka banyaknya kolom juga n, sehingga ordo matriks A adalah n × n. Seringkali matriks A yang berordo n × n dapat disebut dengan matriks persegi ordo n. Elemen-elemen a11, a22, a33, …, ann merupakan elemen-elemen pada diagonal utama.

Contoh :

Matriks Persegi

Elemen – elemen diagonal yang utama matriks A yaitu = 1 dan 10, sedangkan pada matriks B yaitu = 4, 6, 13, dan 2.

4. Matriks Diagonal

Matriks Diagonal yaitu merupakan matriks persegi dengan setiap elemen yang bukan elemen – elemen diagonal yang utamanya adalah 0 (nol), sedangkan elemen pada diagonal yang utamanya tidak semuanya nol.

Contoh :

Matriks Diagonal

5. Matriks Identitas

Matriks Identitas yaitu merupakan matriks persegi dengan semua elemen pada diagonal utama adalah 1 (satu) dan elemen lainnya semuanya 0 (nol). Pada umumnya matriks identitas dapat dinotasikan dengan I dan disertai dengan ordonya.

Contoh :

Matriks Identitas

6. Matriks Nol

Matriks Nol yaitu merupakan suatu matriks yang semua elemennya adalah 0 (nol). Matriks nol biasanya dinotasikan dengan huruf O diikuti ordonya, O_{m x n.}

_{contoh :}

       Matriks Nol

Determinan Matriks

Determinan dari matriks A diberi notasi tanda kurung, sehingga penulisannya |A|. Determinan hanya bisa dilakukan pada matriks persegi.

Determinan matriks ordo 3×3 (aturan Sarrus)

Berikut sifat-sifat determinan matriks:

1. Determinan A = Determinan AT

2. Tanda determinan berubah jika 2 baris/2 kolom yang berdekatan dalam matriks ditukar.

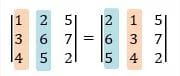
3. Apabila suatu baris atau kolom determinan matriks memiliki faktor p, maka p bisa dikeluarkan menjadi pengali.

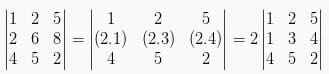
4. Apabila dua baris atau dua kolom merupakan saling berkelipatan, maka nilai determinannya adalah 0.

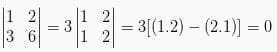
5. Nilai determinan dari matriks segitiga atas atau bawah adalah hasil kali dari elemen-elemen diagonal saja.

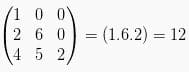
Invers Matriks

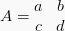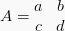Suatu matriks A memiliki invers (kebalikan) jika ada matriks B yang dapat membentuk persamaan AB = BA = I, dengan I adalah matriks identitas. Invers dari suatu matriks berordo (2 x 2) seperti   bisa dirumuskan sebagai :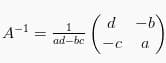

Berikut sifat-sifat invers matriks:

AA-1 = A-1A = I
(A-1)-1 = A
(AB)-1 = B-1A-1Jika AX = B, maka X = A-1B
Jika XA=B, maka X = BA-1

contoh soal:

Contoh matriks menentukan nilai x dengan menggunakan matriks penjumlahan dan pengurangan

Contoh invers matriks :