Elemen dan Himpunan, Bilangan : 2019

INTEGRAL

INTEGRAL

A. Pengertian Integral

Integral adalah kebalikan dari diferensiasial. Apabila fungsi F(x) merupakan integral (anti derivative) function dari fungsi f(x) maka : F(x) disebut sebagai primitive function sedangkan f(x) merupakan derivative dari F(x). Lambang integral adalah “ ∫ “.

Integral terbagi dua yaitu integral tak tentu dan integral tertentu.

1. Integral Tak Tentu

Integral tak tentu adalah integral yang tidak memiliki batas atas dan bawah. Biasanya hanya berupa integral dari sebuah aljabar matematika. Bentuk integral ini tidak memiliki daerah asal dan tidak memiliki daerah hasil

∫ f(x) dx = F(x) + c

2. Integral Tentu

Integral tentu pertama kali diperkenalkan oleh Newton dan Leibinz yang kemudian dieperkenalkan secara modern oleh Riemann. Integral ini memiliki batas atas dan batas bawah. Dalam aplikasinya, integral tentu banyak digunakan untuk menghitung luas di bawah kurva dengan batas tertentu atau menghitung volume benda jika diputar.

B. Aturan-aturan rumus dalam Integral

1. Aturan dasar integral

Aturan ini biasa disebut "The Power Rule", karena aturan ini adalah aturan yang paling umum yang harus dikuasai untuk bisa mengerjakan soal-soal dalam integral.

2. Aturan Eksponensial
Perlu kita ketahui fungsi eksponensial adalah fungsi yang biasa dinotasikan dalam bentuk e^x (e pangkat x), dimana e adalah basis logaritma natural.

3. Aturan Logaritma
Semua perpangkatan dalam integral bisa diselesaikan dengan aturan "the power rule" kecuali pangkat -1. Untuk menyelesaikannya perlu menggunakan aturan logaritma.

4. Aturan dalam operasi
    Aturan ini biasa disebut "Rules Of Operation". Jadi aturan ini mengatakan dalam penjumlahan dari suatu fungsi integral itu sama aja dengan menjumlahkan masing-masing fungsi tersebut.

5. Aturan Konstanta
    Aturan ini mengatakan bahwa apabila dalam integral ada sebuah konstanta dikalikan sebuah fungsi maka konstanta tersebut bisa langsung dikedepankan.

6. Aturan Substitusi
    Aturan ini digunakan ketika proses pengintegralan tidak bisa diselesaikan dengan rumus-rumus dasar integral, atau seandainya bisa diselesaikan namun akan memerlukan proses yang cukup panjang. Suatu metode penyelesaian integral dengan cara substitusi f(x) dengan simbol "U", syaratnya pilih fungsi yang paling rumit.

7. Aturan Parsial
    Aturan ini digunakan untuk soal integral yang sangat kompleks. Biasanya, cara ini digunakan ketika metode yang ada untuk menyelesaikan soal integral tidak bisa digunakan. Soal integral yang dapat diselesaikan menggunakan integral pasrsial terbagi menjadi dua, satu sebagai fungsi u dan satunya sebagai dv. Syaratnya yaitu pilih fungsi yang paling sederhana untuk dijadikan sebagai "U".

8. Aturan Trigonometri
    Aturan trigonometri ini adalah aturan yang paling banyak rumusnya dan harus kalian hafalkan agar bisa menjawab soal-soal. Selain itu bekal untuk mengerjakan integral trigonometri ini kalian juga harus hafal dengan identitas trigonometri.

Dalam integral triogonometri, kita harus menghafalkan beberapa rumus dibawah ini :

a. Identitas Trigonometri

Image result for identitas trigonometri lengkap

b. Rumus Integral fungsi trigonometri

Contoh soal :

MATRIKS III ( PERSAMAAN SIMULTAN DAN ATURAN CRAMER )

MATRIKS LANJUTAN

PERSAMAAN SIMULTAN

Persamaan simultan adalah kumpulan dari beberapa persamaan linear yang terdiri dari satu, dua atau tiga variable bebas. Untuk persamaan linear yang terdiri dari satu variable, misalnya 4x + 5 = 9, maka dengan mudah bisa diselesaikan persamaan tersebut dengan memindahkan ruasnya

Dapat dilihat pada contoh berikut :

4x + 5 = 9 4x = 4 x = 1

Dibawah ini yang akan kita bahas adalah persamaan linear dari 2 dan 3 variabel.

A. Sistem Persamaan Linear Dua Variabel

Tujuan penyelesaian sistem persamaan linear dua variabel adalah menentukan nilai x dan y yang memenuhi sistem persamaan itu. Cara yang paling umum dilakukan untuk menyelesaikan sistem persamaan linear dua variabel (SPLDV) adalah menggunakan metode substitusi, eliminasi, atau campuran. Kali ini, idschool akan mengenalkan cara menyelesaiakan sistem persamaan linear (SPL) dengan cara yang baru, yaitu dengan menggunakan matriks. Meskipun cara ini akan sedikit rumit, namun cara ini akan sangat berguna untuk menyelesaikan sistem persamaan linear dengan banyak variabel. Selanjutnya, langsung ke langkah-langlah penyelesaian SPLDV yang dapat dilihat di bawah.

Diketahui sistem persamaan linear dua peubah sebagai berikut

$ax + by = c$

$px + qy = r$

Dua persamaan di atas merupakan sistem persamaan linear dengan dua variabel, yaitu x dan y. Bentuk sistem di atas dalam matriks bisa dilihat pada persamaan di bawah.

$\begin{bmatrix} a & b \\ p & q \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} c \\ r \end{bmatrix}$

Berdasarkan sifat matriks invertibel, maka variabel x dan y dapat diketahui melalui cara berikut.

$\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} a & b \\ p & q \end{bmatrix}^{-1} \begin{bmatrix} c \\ r \end{bmatrix}$

$\begin{bmatrix} x \\ y \end{bmatrix} = \frac{1}{aq - bp} \begin{bmatrix} q & -b \\ -q & a \end{bmatrix} \begin{bmatrix} c \\ r \end{bmatrix}$

Atau juga bisa dengan cara seperti berikut.

$x = \frac{D_{x}}{D} = \frac{\left| \begin{matrix} c & b \\ r & q \end{matrix} \right| }{\left| \begin{matrix} a & b \\ p & q \end{matrix} \right| }$

$y = \frac{D_{y}}{D} = \frac{\left| \begin{matrix} a & c \\ p & r \end{matrix} \right| }{\left| \begin{matrix} a & b \\ p & q \end{matrix} \right| }$

Contoh soal sistem persamaan linear dua variabel yang diselesaikan menggunakan matriks dapat dilihat pada pembahasan di bawah.
Tentukan nilai x dan y yang memenuhi sistem persamaan linear:

$2x + y = 5$

$x + y = 7$

Selanjutnya, akan diselesaikan SPLDV di atas menggunakan matriks. Bentuk matriks dari persamaan SPLDV pada soal adalah sebagai berikut.

$\begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 5 \\ 7 \end{bmatrix}$

$\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} ^{-1} \begin{bmatrix} 5 \\ 7 \end{bmatrix}$

$\begin{bmatrix} x \\ y \end{bmatrix} = \frac{1}{2 \cdot 1 - 1 \cdot 1} \begin{bmatrix} 1 & -1 \\ - 1 & 2 \end{bmatrix} \begin{bmatrix} 5 \\ 7 \end{bmatrix}$

$\begin{bmatrix} x \\ y \end{bmatrix} = \frac{1}{2 - 1} \begin{bmatrix} 1 & -1 \\ - 1 & 2 \end{bmatrix} \begin{bmatrix} 5 \\ 7 \end{bmatrix}$

$\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ - 1 & 2 \end{bmatrix} \begin{bmatrix} 5 \\ 7 \end{bmatrix}$

$\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -2 \\ 9 \end{bmatrix}$

Jadi, solusi dari dua persamaan linear dua variabel 2x + y = 5 dan x + y = 7 adalah $x = -2$ dan $y = 9$

ATURAN CRAMER

Aturan Cramer untuk Sistem 3 × 3

Aturan Cramer dapat diperluas untuk sistem persamaan linear 3 × 3, dengan menggunakan pola yang sama dengan sistem 2 × 2. Diberikan sistem umum 3 × 3,

Solusi-solusi dari sistem tersebut adalah x = Dx/D, y = Dy/D, dan z = Dz/D, dimana Dx, Dy, dan Dz dibentuk dengan mengganti koefisien variable-variabel yang bersangkutan dengan konstanta, dan D adalah determinan dari matriks koefisien (D ≠ 0).

Penerapan Aturan Cramer untuk Sistem 3 × 3

Diberikan suatu sistem persamaan linear 3 × 3

Solusi dari sistem tersebut adalah (x, y, z), dimana

dengan syarat D ≠ 0.

Contoh 2: Menyelesaikan Sistem 3 × 3 Menggunakan Aturan Cramer

Selesaikan sistem berikut dengan menggunakan aturan Cramer.

Pembahasan Pertama kita tentukan determinan dari matriks koefisien untuk memastikan apakah aturan Cramer dapat diterapkan atau tidak. Dengan menggunakan baris ketiga kita mendapatkan

Karena D ≠ 0, kita lanjut untuk menentukan determinan dari matriks-matriks lainnya dengan menggunakan Ms. Excel (rumus untuk menentukan determinan dalam Ms. Excel adalah “=MDETERM(array)”).

Sehingga kita memperoleh,

Jadi, selesaian dari sistem tersebut adalah (2, 0, –1).

Menyelesaikan SPLTV dengan Matriks

Cara menyelesaikan sistem persamaan linear menggunakan matriks akan sangat bermanfaat pada sistem persamaan linear dengan variabel yang banyak, misalnya pada sistem persamaan linear tiga variabel (SPLTV). Metode substitusi, eliminasi, atau campuran dirasa tidak tepat untuk menyelesaikan SPLTV. Selanjutnya, simak penyelesaian sistem persamaan linear tiga variabel (SPLTV) menggunakan matriks.

Diketahui tiga persamaan linear dengan tiga variabel (x, y, dan z) seperti terlihat pada persamaan di bawah.

$ax + by + cz = d$

$px + qy + rz = s$

$kx + ly + mz = n$

Bentuk SPLTV di atas dalam bentuk matriks dapat dibuat seperi berikut.
Cara Menyelesaikan Sistem Persamaan Linear (SPL) dengan Matriks

Berdasarkan matriks di atas, dapat disusun determinan utama, determinan variabel x, determinan variabel y, dan determinan variabel z. Untuk lebih jelasnya perhatikan masing-masing determinan pada daftar di bawah.

Contoh soal :

MATRIKS Lanjutan II ( DETERMINAN DAN EKSPANSI LAPLACE )

MATRIKS (Lanjutan)

Determinan

Pengertian determinan :

Determinan merupakan sebuah bilangan tunggal atau scalar, dan hanya dijumpai dalam matriks bujur sangkar. Jika determinan suatu matriks bujur sangkar adalah nol, maka matriks tersebut dikatakan sebagai matriks singular. Dan jika determinan matriks tersebut bukan nol, maka matriks tersebut dikatakan sebagai matriks non singular. Matriks nonsingular, secara linear tidak tergantung (saling independent)

Determinan Matriks Ordo 2 x 2

Jika diberikan matriks ordo 2 dinyatakan seperti bentuk di bawah.

Sifat-sifat Determinan :

Sifat-sifat determinan ada enam, yaitu :

a. Determinan suatu matriks sama dengan determinan dari transposenya, det (A) = det (A^t).

Contoh :

b. Penambahan atau pengurangan suatu kelipatan bukan nol dari suatu baris/kolom dari baris/kolom lainnya tidak akan mempunyai pengaruh pada determinan.

c. Penukaran tempat antara dua baris atau kolom sembarang dari suatu matriks akan merubah tanda, tetapi tidak merubah harga absolut dari determinan.

Contoh :

d. Determinan dari suatu matriks segitiga (triangular matriks), yaitu matriks dengan elemen-elemen nol diatas atau di bawah diagonal utama, adalah sama dengan hasil kali dari elemenelemen dari diagonal utama.

Contoh :

e. Jika semua elemen dari suatu baris atau kolom adalah nol, determinan adalah nol.

Contoh :

f. Jika dua baris atau kolom identik, atau proporsional, yaitu secara linear tergantung, maka determinan adalah nol.

Contoh :

METODE MINOR DAN KOFAKTOR

Salah satu cara menentukan determinan matriks segi adalah denga minor-kofaktor elemen matriks tersebut.

Cara ini dijelaskan sebagai berikut:

Misalkan

A_{i j}

adalah suatu matriks yang diperoleh dengan cara menghilangkan baris ke-i dan kolom ke-j dari suatu matriks

A_{m x n}

Didefinisikan sebagai berikut:

Minor elemen $a_{i j}$ diberi notasi $M_{i j}$ , adalah $M_{i j} = d e t (A_{i j})$ .
Kofaktor elemen $a_{i j}$ , diberi notasi $α_{i j}$ , adalah $α_{i j} = (- 1)^{i + j} M_{i j}$ .

Contoh:

Misalkan suatu matriks A berukuran 3x3 seperti berikut ini:

(\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix})

maka diperoleh:

Perhitungan Determinan dengan Minor-Kofaktor

Definisi: Misalkan suatu matriks A =

(a_{i j})_{n x n}

dan

a_{i j}

kofaktor elemen

a_{i j}

, maka:

Ekspansi Laplace

Metode atau ekspansi Laplace adalah suatu cara untuk menghitung determinan dengan menggunakan kofaktor.

Determinan dari suatu matriks = jumlah perkalian elemen-elemen dari sembarang baris/kolom dengan kofaktor-kofaktornya.

Ekspansi Laplace dapat ditulis dengan cara :

|A| = a11|C11|+a12|C12|+a13|C13| menggunakan baris 1

Dengan pola yang sama dapat juga dihitung dengan menggunakan baris ke dua dan ketiga, dengan memberikan hasil determinan yang sama.

Contoh soal :

Senin, 16 Desember 2019

INTEGRAL

Integral terbagi dua yaitu integral tak tentu dan integral tertentu.

1. Integral Tak Tentu

2. Integral Tentu

1. Aturan dasar integral

Aturan ini biasa disebut "The Power Rule", karena aturan ini adalah aturan yang paling umum yang harus dikuasai untuk bisa mengerjakan soal-soal dalam integral.

2. Aturan Eksponensial Perlu kita ketahui fungsi eksponensial adalah fungsi yang biasa dinotasikan dalam bentuk e^x (e pangkat x), dimana e adalah basis logaritma natural.

MATRIKS III ( PERSAMAAN SIMULTAN DAN ATURAN CRAMER )

Menyelesaikan SPLTV dengan Matriks

MATRIKS Lanjutan II ( DETERMINAN DAN EKSPANSI LAPLACE )

2. Aturan Eksponensial
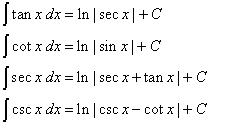
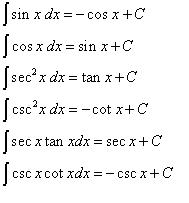
Perlu kita ketahui fungsi eksponensial adalah fungsi yang biasa dinotasikan dalam bentuk e^x (e pangkat x), dimana e adalah basis logaritma natural.